代码随想录-动态规划基础
动态规划五部曲
1.确定dp数组以及下标的含义
2.确定递推公式
3.dp数组如何初始化
4.确定遍历顺序
5.举例推导dp数组
509.斐波那契数
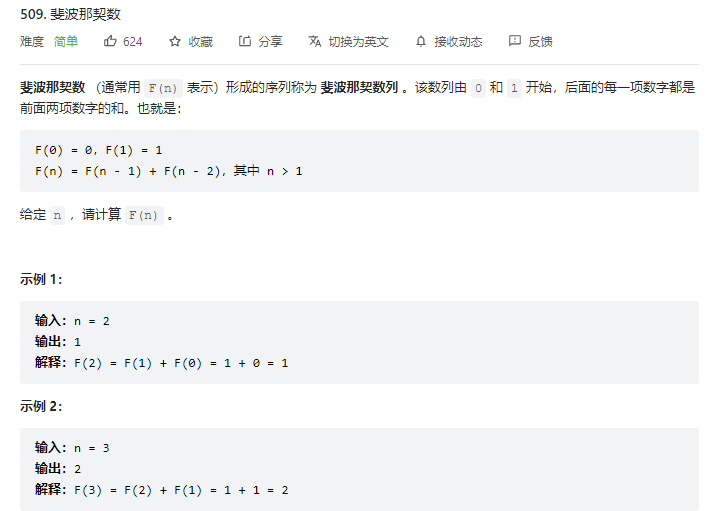
动规解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34/**
* @param {number} n
* @return {number}
*/
/**
* 动态规划五部曲
1.确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
2.确定递推公式
题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
3.dp数组如何初始化
dp[0] = 0;dp[1] = 1;
4.确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2]中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
5.举例推导dp数组
0 1 1 2 3 5 8 13 21 34 55
*/
var fib = function(n) {
if(n < 2){
return n
}
// 1.确定数组下标 :dp[i]为斐波那契数列的第i项
let dp = []
// 3.初始化
dp[0] = 0
dp[1] = 1
// 4.遍历顺序
for(let i = 2; i <= n; i ++){
// 2.递推公n
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n]
};当然,这题用递归超简单
1
2
3
4
5
6
7
8
9
10
11
12/**
* @param {number} n
* @return {number}
*/
var fib = function(n) {
if(n < 2){
return n
}
return fib(n - 1)+ fib(n - 2)
};
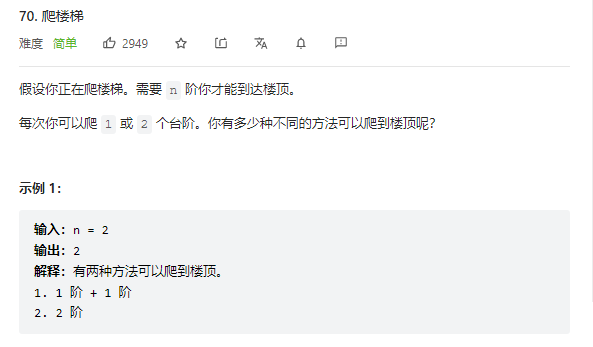
70.爬楼梯
1 | /** |
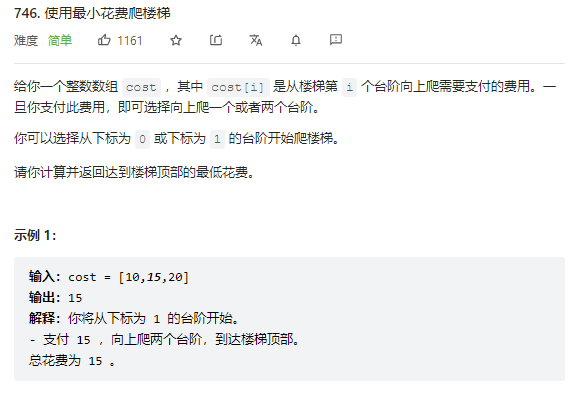
746.使用最小花费爬楼梯
1 | /** |
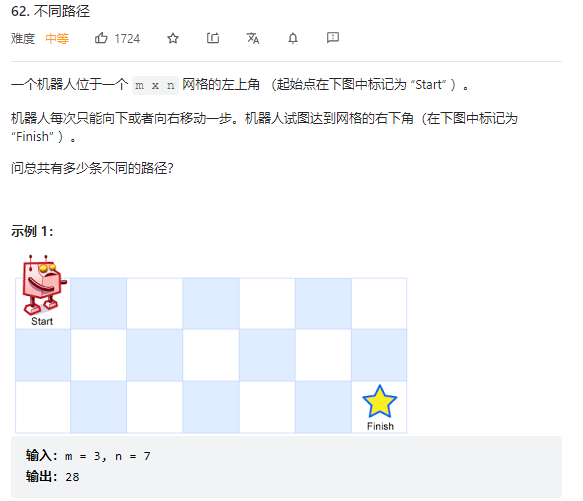
62.不同路径
1 | /** |
63.不同路径Ⅱ
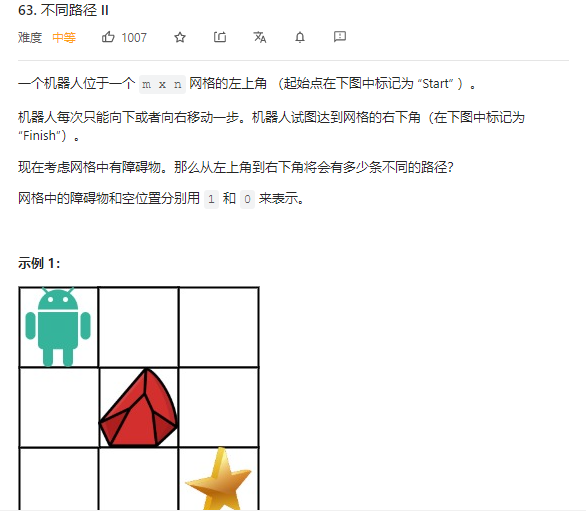
动态规划 初始化比较麻烦
1 | /** |
343.整数拆分
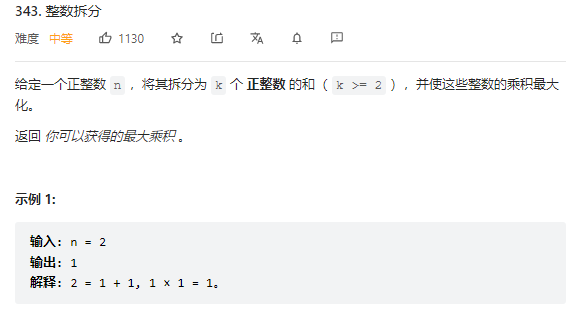
动态规划 比较难想
1 | /** |
96.不同的二叉搜索树
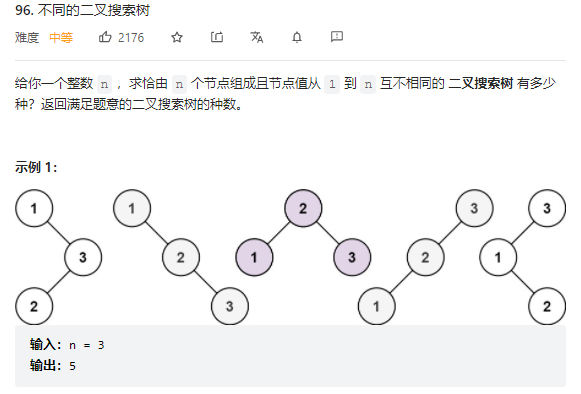
动态规划 递推公式很困难,需要了解搜索二叉树
1 | /** |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 罗辑往事!


